|
Análisis de las incertidumbres, asociadas a las hipótesis de calculo, en la estimación de curvas de gasto para crecidas, basada en el empleo de modelo matemático de cálculo hidráulico en régimen permanente |
ANGEL LUIS ALDANA VALVERDE (*); JUAN CARLOS GONZÁLEZ RODRIGUEZ (**)
| RESUMEN Se analizan en este artículo algunos de los factores más importantes que pueden afectar a los resultados de cálculo de láminas de agua en un río para diferentes caudales bajo la hipótesis de régimen permanente. En este caso, el objetivo de este tipo de modelización ha sido la estimación de curvas de gasto para avenidas en las estaciones de aforo conectadas al sistema automático de información hidrológica (SAIH) de la Confederación Hidrográfica del Sur de España (CHSE), sistema conocido como red Hidrosur. | |
ANALYSIS OF UNCERMIES, ASSOCIATED TO THE CALCULATING HYPOTHESIS, IN DISCHARGE TABLES FOR HIGH FLOWS ESTIMATING, BASED ON MATEMATHICS MODELS FOR CALCULATING WATER SURFACE PROFILES FOR STEADY GRADUALLY VARIED FLOW ABSTRACT In this paper are analyzed some of the most important factors which can influence on the results of calculating water surface profiles for steady gradually varied flow. In this case, the objective of this hind of modeling, has been the estimation of discharges tables for high flows of river station gages connected to the hydrologic automatic information system (SA1H) of the Confederación Hidrográfica del Sur de España, system named "red Hidrosur". |
Palabras clave: Hidrometría; Hidráulica; Tiempo real; SAIH.
Los modelos matemáticos pueden proporcionar una aproximación suficiente en la mayoría de los casos de aplicación práctica, según la finalidad última de la utilización de los resultados. En este caso, los trabajos realizados tenían como objetivo la estimación de curvas de gasto para ser usados en situaciones de avenida como dato de entrada al modelo de previsión en estaciones de aforos CRAF en la red Hidrosur.
El método alternativo a la utilización de un modelo matemático es el del aforo directo, midiendo velocidades en diferentes puntos de la sección en la que se desea estimar la relación entre caudales y niveles, pero esto es difícil de llevar a cabo en la práctica y es raro encontrar este tipo de medida en ríos como los que aquí se tratan, por encontrarse en cuencas con fenómenos hidrológicos que a menudo presentan un carácter torrencial y que, al menos, responden a la lluvia de forma rápida.
Los trabajos de los que se extraen las conclusiones que aquí se presentan fueron realizados en el marco del convenio firmado entre la Confederación Hidrográfica de¡ Sur de España (CHSE) y el Centro de Estudios y Experimentación de Obras Públicas (CEDEX) titulado "Convenio para la realización de trabajos de asistencia técnica en la implantación de modelos hidrológicos y de gestión hidráulica en la red Hidrosur". En la actualidad estas curvas están siendo usadas en la previsión de avenidas en tiempo real como un dato más para el citado modelo de previsión.
2. CARACTERÍSTICAS BASE TEÓRICA Y LIMITACIONES DEL MODELO EMPLEADO
El software empleado para la realización de los cálculos de la lámina de agua es el denominado HEC-Ras, del Centro de Ingeniería Hidrológica (Hydrologic Engineering Center) del Cuerpo de Ingenieros de la Armada de los EE.UU. (US Army Corps of Engineers), que parte del conocido y ampliamente utilizado HEC-2, con varias mejoras con respecto a éste, entre las que destaca la interfase gráfica de usuario que facilita las labores de preproceso y postproceso. Este software permite el tratamiento de singularidades tales como puentes y su uso está muy extendido.
El modelo numérico incluido en este programa informatico, permite realizar análisis del flujo permanente unidimensional gradualmente variado en lámina libre. Para su utilización se han de definir unas secciones transversales que representan una discretización del tramo o tramos a analizar.
La mayor parte de las limitaciones del modelo vienen derivadas de las hipótesis propias del modelo numérico, generales a los modelos matemáticos habitualmente empleados.
En primer lugar hay que recordar que el modelo de análisis que se emplea, opera bajo la hipótesis de régimen permanente, lo que conduce a resultados aceptables cuando no hay variaciones importantes en los hidrogramas de entrada al modelo, de tal forma que sean despreciables los términos inerciales de las ecuaciones completas de la hidráulica. Diferirá más de la realidad, cuanto más bruscas sean estas variaciones, o cuando los valores de los sumandos despreciados tengan una importancia relativa alta. En estos casos suelen observarse en la realidad fenómenos de histéresis notables.
Este tipo de modelo no tiene en cuenta el transporte de sólidos, lo que puede ser otra de las causas que desvíen los resultados del modelo de la realidad. De producirse en el tramo de estudio un transporte importante de sólidos, por arrastre o suspensión, los calados necesarios para conducir iguales caudales líquidos serán mayores. Además, en la realidad, sobre todo para los caudales mayores que moverán cantidades más importantes de sólidos, pueden observarse modificaciones de la geometría del cauce que repercutan de forma notable en su comportamiento hidráulico.
Cuando los modelos numéricos tratan de resolver el problema hidráulico en situaciones en las que se presenta el régimen crítico, cuentan con la dificultad añadida de que en estos casos, las hipótesis implícitas en las ecuaciones básicas no son del todo ciertas, pues las líneas de corriente presentan en la realidad fuertes curvaturas, es decir, no son ciertas las hipótesis de régimen gradualmente variado. Cuando se presenta este régimen, se observan inestabilidades que suelen manifestarse como ondulaciones en superficie.
Se analizan en los siguientes apartados un conjunto de factores que dependen bien de las ecuaciones del modelo, de los algoritmos de cálculo, de los parámetros de modelización o de la información de que se dispone y sirve de entrada al modelo. En concreto se tratan:
Modo de cálculo.
Rugosidad.
Distribución transversal de caudales.
Condición de contorno.
Modificación de geometría.
Además se reflexiona en un apartado sobre un tema que afecta especialmente al objetivo de estos cálculos: la diferencia entre la realidad y los resultados del modelo matemático en lo concerniente al régimen crítico.
El modelo empleado da opción a que el usuario elija entre tres modos de cálculo: subcrítico, supercrítico y mixto. Para el primer modo (modo correspondiente a la hipótesis de flujo en régimen lento, también denominado subcrítico) se realizan cálculos partiendo de la condición de contorno en la sección más aguas abajo, avanzando hacia aguas arriba, contrariamente a lo que se hace en el modo supercrítico (régimen rápido), pues en este caso se parte de la condición de contorno en el extremo aguas arriba avanzando hacia aguas abajo. Además, este modelo proporciona el modo de cálculo denominado mixto, en el cual el algoritmo de cálculo realiza varias pasadas en ambos sentidos buscando los cambios de régimen, situando y calculando los resaltos hidráulicos.
Como ejemplo de análisis de diferencias de los cálculos en este modo respecto a alguno de los anteriores, se cita la aplicación del modelo en la estimación de la curva de gasto para avenidas en la estación de aforos que se encuentra en el río Almanzora a su paso por el término de Cantoria (Almería).
 |
FIGURA 1. Almanzora en Cantoria. Perspectiva de la estación de aforos. |
El régimen de flujo que se deduce de los cálculos es subcrítico muy próximo al crítico. A causa de esto puede que se presenten resaltos que se manifestarán como ondulaciones de la lámina. El modelo, al realizar cálculos en modo mixto, sitúa resaltos, claramente definidos para caudales altos, aguas arriba del puente, tal y como puede apreciarse en el gráfico de perfiles longitudinales de las láminas de agua para los diferentes modos (Figura 2), en la que se presentan los resultados de los cálculos realizados en modo mixto (azul) y subcrítico (verde) para caudales de 25, 150 y 300 m3/s.
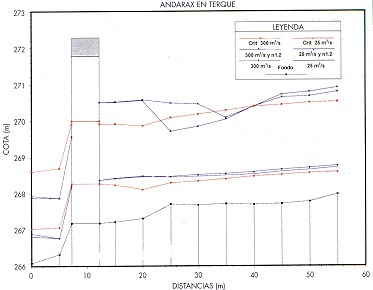 |
FIGURA 2. Almanzora en Cantoria. Cálculos realizados en modo mixto (azul) y subcrítico (verde) para caudales de 25, 150 y 300 m3/s. |
En cualquier caso, en la zona próxima a la sección de medida, el calado es muy próximo al crítico en todas las hipótesis contempladas en el estudio, lo que permite realizar una estimación de la relación nivel-caudal en este punto, excepto para los caudales mayores por lo que, como se verá sucesivos apartados, se contará para ellos con otras incertidumbres.
Cuando el régimen del flujo en el tramo de estudio sea próximo al crítico, apenas se apreciarán cambios en los resultados de cálculo al variar la rugosidad, como es el caso de la estación de aforos del río Andarax en el término municipal de Terque, para el que se muestran los resultados de incrementar un 20% los valores de rugosidad supuestos. Sin embargo, tal y como puede comprobarse en el gráfico adjunto, el incremento de rugosidad sí afecta a lo concerniente a la formación del resalto hidráulico en los caudales mayores (Figura 3).
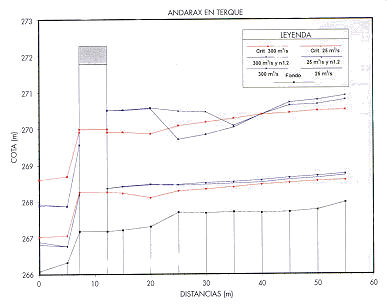 |
FIGURA 3. Andarax en Terque. Efecto de la rugosidad |
En un caso en el que el régimen de circulación del agua sea muy distinto al crítico, el efecto de la rugosidad puede ser importante, como se aprecia en el gráfico adjunto de resultados de cálculos (Figura 4) de la modelización de la estación de aforos de la rambla de Tabernas, situada en el término de Tabernas, en el que se muestran los resultados de cálculo correspondientes a la rugosidad inicialmente supuesta y a los correspondientes a un incremento del 20% sobre la inicialmente supuesta, además de las láminas de agua que corresponderían a los calados críticos para cuatro caudales. El fondo del cauce en la zona de esta estación se encuentra cubierto de abundante vegetación, por lo que se le ha asignado un alto valor a la rugosidad, y en ella el agua circula en claro régimen subcrítico.
FIGURA 4. Rambla de Tabernas. Efecto de la rugosidad |
 |
Este efecto podría suprimirse o al menos limitarse, si al final de la estación de aforos, en su extremo aguas abajo, se mantuviera el escalón con el que la estación se proyectó y construyó, hoy inexistente a causa de las sedimentaciones y que podría reconstruirse con unas sencillas labores de mantenimiento de la estación. De este modo se lograría que el agua alcanzase el régimen crítico a su paso por la estación.
3.3. DISTRIBUCIÓN TRANSVERSAL DE CAUDALES (GENAL EN ALGATOCÍN Y JUBRIQUE)
En algunas ocasiones se puede dar la circunstancia de que se desee estimar la lámina de agua a que daría lugar un determinado caudal y que para esta lámina la cartografía de que se dispone resulte insuficiente. Si se conoce la zona, gracias a la obligada visita al lugar, quizás sean admisibles extrapolaciones de esta cartografía si el análisis de la influencia que el error que en esta operación se produzca tiene poca repercusión en los resultados de cálculo. Tal es el caso de la estación de aforos del río Genal que se encuentra en el límite municipal de las poblaciones de Algatocín y Jubrique (Málaga), en el puente que une ambas, en el que se detectó insuficiente la cartografía por ambas márgenes, aunque esto no tuvo apenas influencia en la curva estimada gracias a la distribución de caudales en la sección transversal, que aunque es un resultado de cálculo discutible en los aspectos cuantitativos, desde el punto de vista cualitativo es totalmente admisible.
 |
FIGURA 5. Genal en Algatocín y Jubrique. Perspectiva de la estación de aforos |
La abundante y espesa vegetación de la zona dificulta el flujo del agua especialmente en las márgenes, fuera de lo que se ha considerado el cauce principal (zona media de la sección), por lo que el caudal en el canal central es mucho mayor que en las márgenes, según puede verse en la figura adjunta (Figura 6) que corresponde a un caudal total que se ajusta a la extensión de las secciones incluida en la cartografía disponible, lo que justifica que se acepten resultados de cálculos para caudales que proporcionen alturas de lámina algo superiores a lo que alcanza esta cartografía, bajo el supuesto de que no se producen desbordamientos u otros efectos importantes.
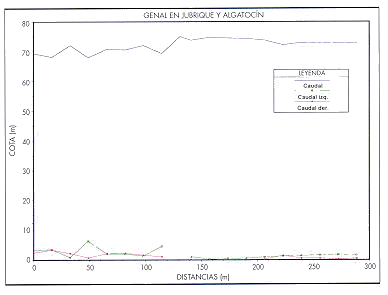 |
FIGURA 6. Distribución de caudales en la sección transversal en el río Genal |
3.4. CONDICIÓN DE CONTORNO (GUADALFEO EN LOBRAS)
La condición de contorno del problema de modelación hidráulico de un tramo de río puede ser otra de las incógnitas o, al menos, puede tener asociada una incertidumbre alta. Ante esta situación, que debe evaluarse siempre, hay que evaluar la repercusión que el error en la estimación de condición de contorno pueda tener en los resultados finales a los que se pretende llegar: la estimación de la relación de calados con caudales, en este caso.
FIGURA 7. Guadalfeo en Lobras. Perspectiva de la estación de aforos |
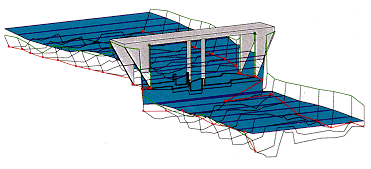 |
Como ejemplo se muestra el caso de la estación del río Guadalfeo que se encuentra en el término municipal de Lobras (Granada). En el tramo estudiado el agua fluye en régimen supercrítico, pudiéndose formar un resalto hidráulico aguas arriba del puente para caudales superior a los 100 m 3/s, atravesando el puente en régimen crítico. Al realizar un análisis de la influencia de la condición de contorno, impuesta en la sección aguas arriba, sobre la sección de medida se concluye en que la afección es nula, tal y como puede comprobarse en el gráfico de resultados de este análisis (Figura 8), que muestra las láminas resultantes del cálculo bajo la hipótesis de condición dada por el calado crítico y la correspondiente a calado uniforme.
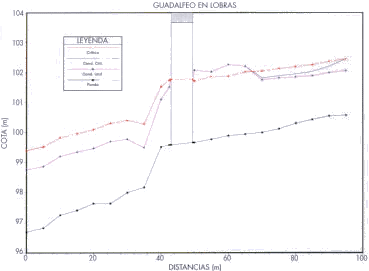 |
FIGURA 8. Guadalfeo en lobras. Influencia de la condición de contorno (para caudal de 200 m3/s) |
Sin embargo, en el caso antes mencionado de la estación de la rambla de Tabernas, dado que el agua fluye en un régimen distinto del crítico y no alcanza este régimen en la zona de medida, esta incertidumbre se superpondría a otras.
3.5. MODIFICACIÓN DE GEOMETRÍA (NACIMIENTO EN TERQUE)
La geometría del cauce puede sufrir modificaciones por efecto de una avenida, por lo que la definición de ésta, aparte de otros posibles errores, puede ser otra de las incertidumbres con que hay que contar en al menos aquellos casos en los que esto sea previsible. Tal es el caso del tramo del río Nacimiento estudiada para la estimación de la curva de gasto para avenidas en la estación de aforos situada en este río.
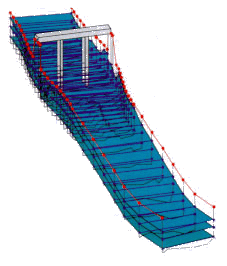
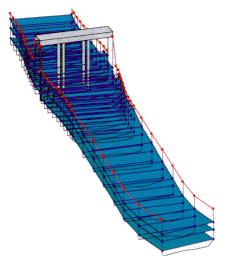
Su geometría presenta muchas irregularidades en su fondo que probablemente desaparezcan al paso de una avenida, por lo que se ha realizado una prueba de cálculo suponiendo que se suaviza tal y como muestran las figuras adjuntas (Figura 9 yFigura 10).
 |
|
FIGURA 9. Nacimiento en Terque. Perspectiva con geometría actual | FIGURA 10. Nacimiento en Terque con geometría modificada |
Las diferencias que se detectan son pequeñas (Figura 11), repitiéndose los mismos fenómenos en torno al puente (donde está situada la estación) para una y otra geometría.
 |
FIGURA 11. Nacimiento en Terque. Efecto de la modificación de la geometría |
3.6. CONSIDERACIONES SOBRE LA POSICIÓN DE LA SECCIÓN CON CALADO CRÍTICO
El modelo matemático fija una sección con calado crítico que puede no coincidir con la realidad. En relación con esto hay que recordar lo mencionado anteriormente sobre el cálculo hidráulico en régimen crítico, pues contradice las hipótesis básicas de las ecuaciones, lo que se manifiesta en estas diferencias.
En la realidad puede darse la circunstancia que no se presente una sección con este régimen claramente definido, sino que exista una zona de río con un número de Froud que oscila con valores próximos a la unidad a lo largo de su longitud. En otros casos, como el que se presenta en estaciones en las que el modelo fija el calado crítico en su extremo aguas abajo, inmediatamente antes del escalón que le suele seguir, puede presentarse en la realidad aguas arriba de este extremo, lo que suele ocurrir en estaciones en las que el agua llega en régimen subcrítico y hay espacio suficiente como para que adquiera velocidad.
Teniendo en cuenta el objetivo final del uso de los modelos matemáticos, éstos pueden ser una herramienta útil para la estimación de curvas de gasto para avenidas a pesar de las incertidumbres con que se cuenta, siempre que tras el análisis de las mismas se deduzca un error admisible.
Podría ocurrir que de este análisis se llegue a la conclusión de que este método de estimación no sea admisible por el error que lleve asociado, bien por la importancia de alguno de los factores antes tratados o por la superposición de algunos de éstos, o bien porque las hipótesis básicas del modelo no se cumplan. En alguno de estos casos habría que buscar datos adicionales para calibrar el modelo o recurrir a otro método, que bien podría ser el que recurriese al empleo de un modelo físico que serviera para salvar las deficiencias del modelo matemático analizando y cuantificando los fenómenos que este último no puede reproducir, es decir, con la utilización simultánea de modelación física y matemática.
| BIBLIOGRAFÍA |
| VEN TE CHOW, 1994: "Hidráulica de canales
abiertos". Mac Graw Hill. HEC, 1997: "Hydraulic Reference Manual". Hydrologic Engineering Center. US Army Corps of Engineers. 609 Second Street. Davis, CA 95616. CEDEX, 1997: "Aplicación CRAF. Versión 1.0. Manual del usuario." |
(*)
Doctor Ingeniero de Caminos, Canales y Puertos. CEH-CEDEX (Ministerio de Fomento).
(**) Licenciado en Ciencias Químicas. Fundación Aguastín
de Bethancourt.
| SUMARIO | |