|
|||||||||||||||||||||||||
Pilar Brufau García (*), Pilar García Navarro (**)
Palabras
clave: Flujo de superficie libre, modelo hidráulico,
flujo transitorio, rotura de presa.
En muchos países, las leyes obligan a realizar un completo estudio de los parámetros relevantes de la onda que se produce tras la rotura de una presa [1,11] y de la evolución de niveles y caudales en los ríos y embalses como prevención en casos de inundación. Algunos de estos estudios se completan con la realización de un modelo físico a escala del valle para intentar predecir lo que ocurriría en un caso real con las limitaciones asociadas al cambio de escala dinámica. Este procedimiento experimental representa un esfuerzo económico importante y no carente de dificultades. Por ello es cada vez más común estudiar el comportamiento del agua usando simulaciones mediante modelos que aproximan los procesos físicos que tienen lugar. El ordenador constituye una herramienta esencial para facilitar estos cálculos.
Una simulación numérica tiene que describir un fenómeno particular con la suficiente precisión y con un coste bajo para ser de utilidad. Normalmente la precisión y el coste son magnitudes opuestas a la hora de diseñar un esquema numérico. En principio, la precisión del modelo puede aumentar indefinidamente pero en la práctica tiene que existir un compromiso entre la precisión en la descripción del proceso físico y el conocimiento disponible de las leyes físicas básicas del problema particular a resolver. Hay una gran diversidad entre las necesidades y las posibilidades de la simulación numérica y una consecuencia de ello es que en la práctica se utilizan un gran número de métodos numéricos diferentes. Existe un gran número de técnicas numéricas apropiadas para resolver flujos suaves; sin embargo, el caso de resolver un flujo general ha sido tradicionalmente difícil de tratar con un sólo método.
Algunas situaciones hidráulicas pueden ser descritas por medio de un modelo unidimensional, bien porque no sea necesaria la resolución en más detalle del flujo o porque la naturaleza del mismo sea marcadamente unidimensional, como el flujo en un canal [4]. Cuando se intenta hacer uso de los modelos matemáticos como herramienta de predicción en la simulación de flujos de superficie libre, estas hipótesis de aproximación unidimensional no son siempre válidas. Esto ocurre en el caso de que se tenga una geometría totalmente irregular en el cauce, contracciones y expansiones abruptas o ríos con curvatura importante. Cuando se intentan reproducir este tipo de situaciones hidráulicas se hace necesario el uso de un formalismo bidimensional que tenga en cuenta la influencia de las componentes transversales del flujo.
Aunque la simulación matemática ha avanzado significativamente durante los últimos años, la calibración de los modelos de rotura de presa es difícil. Esta es la razón por la cual LNH ha promovido la colaboración de grupos de trabajo en la sección de Hidráulica Fluvial de la IAHR. Este trabajo empezó en 1995 y continuó en una acción concertada europea para la simulación de roturas de presa (CADAM). El programa fue financiado por la Comunidad Europea y sus objetivos han sido: intercambiar información entre los participantes (universidades, organizaciones dedicadas a la investigación, industria); promover la comparación de modelos numéricos de rotura de presa con datos experimentales; validar paquetes comerciales de software o los desarrollados por los propios participantes y promover la investigación conjunta. El programa, que finalizó en 1999, ha servido para desarrollar el código SIBILL y los dos casos de simulación que aquí se presentan fueron suministrados por participantes de la Acción Concertada.
El movimiento del fluido se supone gobernado por los principios fundamentales de conservación de la masa y segunda ley de Newton en dos direcciones horizontales. Esta aproximación lleva asociadas una serie de hipótesis que definen el modelo de aguas poco profundas (shallow water). De entre ellas, es destacable la de distribución hidrostática de presiones. En términos matemáticos, adoptan la forma de ecuaciones en derivadas parciales. Se trata de un sistema hiperbólico no lineal de leyes de conservación.
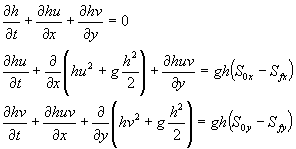
donde h representa la profundidad del agua, hu y hv son los caudales unitarios a lo largo de las direcciones coordenadas x, y respectivamente, Sox, S0y dan cuenta de las variaciones del fondo del cauce en forma de pendiente y Sfx, Sfy constituyen los términos de fricción del agua con el fondo del cauce en cada una de las direcciones coordenadas. La fricción se modela a partir de leyes semi-empíricas importandas de la teoría capa límite bidimensional en equilibrio. Son necesarias condiciones iniciales y de contorno para la resolución del sistema. En situaciones generales no existen soluciones analíticas del problema y se recurre a los métodos numéricos.
El dominio donde se mueve el flujo, se subdivide (discretiza), en un conjunto de celdas para su resolución numérica. Se aplican las leyes de conservación para determinar las variables del flujo en los nodos o en los centros de las celdas, según el método numérico utilizado. En el modelo presentado hay libertad a la hora de elegir el tipo de celdas: hexágonos, cuadriláteros, triángulos, etc... y además pueden formar parte de una malla estructurada o de una malla no estructurada. La elección de la malla para discretizar el flujo es un factor importante en la simulación numérica. Las mallas no estructuradas suponen un gran avance en el análisis del flujo en varias dimensiones; particularmente por su flexibilidad cuando se construyen mallas ajustadas a un contorno en casos de geometrías complejas y, en general, porque muestran ausencia de direcciones privilegiadas en la malla como se verá en los resultados.
Respecto a la técnica de resolución de las ecuaciones, se han usado métodos de volúmenes finitos porque tratan de combinar lo mejor de los métodos de elementos finitos, su flexibilidad geométrica, con lo mejor de los métodos en diferencias finitas, su flexibilidad en la definición del flujo discreto (valores discretos de las variables dependientes y sus flujos asociados).
Los esquemas clásicos unidimensionales, basados en diferencias centradas, dominan los productos comerciales de software que existen en el mercado en el campo de la simulación del flujo de superficie libre en volúmenes finitos: Lax-Friedrichs, Lax-Wendroff, MacCormack, Preissman. Los esquemas explícitos descentrados (upwind) han sido usados con resultados satisfactorios para resolver las ecuaciones de aguas poco profundas unos años después de haberse empleado en la resolución de problemas dentro del dominio de la dinámica de gases [12,13]. La no linealidad del sistema de ecuaciones de aguas poco profundas puede hacer que la solución sea bastante complicada con la aparición de discontinuidades, reflejando fenómenos físicos como saltos hidráulicos y frentes de onda. La técnica numérica adoptada determina la calidad de los resultados y en este caso las ventajas obtenidas en los dos campos (dinámica de gases e hidráulica) son similares [6,7,10].
Algunas de las aproximaciones bidimensionales para problemas hidráulicos que se han llevado a cabo están basadas en la resolución de la ecuación de continuidad junto a conexiones hidráulicas para conocer el caudal (GISPLANA) [5]. Dentro de las aproximaciones que contemplan el modelo dinámico completo, algunas se basan en la técnica operator splitting [6]. Otras técnicas implican el uso del método de características en 2D [8], técnicas eulerianas-lagrangianas [3] o técnicas de elementos finitos [9]. Los métodos de descentramiento son muy populares a la hora de simular flujos en los que domina marcadamente el término advectivo [2] y en particular aquellos que contienen discontinuidades muy fuertes.
La presencia de pendientes elevadas, valores altos de rozamiento y cambios fuertes dentro de una geometría irregular representan una dificultad que puede conducir a importantes errores numéricos presumiblemente producidos por el tratamiento numérico de los términos fuente. Recientes contribuciones en el estudio de problemas con términos fuente ponen de manifiesto que están presentes en gran número de problemas de interés tecnológico. Vázquez-Cendón ha propuesto una metodología general, para extender algunos de los esquemas descentrados clásicos al caso de leyes de conservación con términos fuente [14]. Partiendo de este trabajo, se han usado técnicas especiales de descentramiento para la discretización de los fondos irregulares.
Debido a los valores iniciales en problemas de avance sobre fondo seco y en el caso en que se tenga un valor muy alto de rugosidad (al querer representar los efectos que producen la vegetación, una composición del suelo especialmente rugosa o un fondo de un cauce real de un río), los términos de fricción se vuelven dominantes en el problema y pueden añadir errores numéricos en los resultados. Para evitar este problema, lo que se ha hecho es aproximar los términos de fricción en una forma semi-implícita.
La construcción y las medidas experimentales del caso test que se presenta fueron realizadas por A. Bento en el Laboratorio Nacional de Ingeniería Civil en Portugal. Se obtuvieron datos experimentales en una instalación construida para la simulación de flujos transitorios producidos por una rotura de presa. El mecanismo que se adoptó para simular experimentalmente el fenómeno de la rotura de presa fue usar una compuerta de tipo guillotina en la cual al caer un peso provoca el ascenso de la compuerta. El tiempo total de apertura fue aproximadamente de 0.2s con lo cual se puede considerar instantánea. Las paredes del canal tienen una altura de 0.5m y está construido con hormigón salvo una de sus paredes laterales que es de plexiglás para poder observar y tomar medidas de la evolución del flujo. El canal aguas abajo se abre repentinamente en una llanura. La onda generada por la rotura de la presa inicialmente se propaga por el canal rectangular e inmediatamente entra en una llanura rectangular procediendo a inundarla. El flujo que se produce en esta llanura es de características bidimensionales y se puede comprobar en las múltiples reflexiones que se producen en las paredes laterales que la rodean.
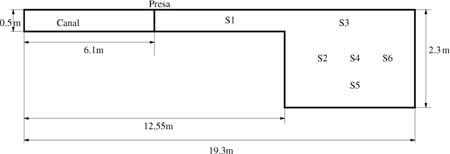
FIGURA
1. Vista en planta de montaje
El modelo físico se esquematiza en la Fig. 1. Consiste en un canal sin pendiente, que tiene una longitud de 19.3m y sección rectangular con una anchura de 0.5m. La posición de la presa se encuentra a 6.1m respecto al origen y la llanura se encuentra situada 6.45m aguas abajo de la compuerta. La llanura que se va a inundar es rectangular con dimensiones: 6.75m de longitud y 2.3m de anchura. Las condiciones iniciales son de flujo estacionario con un nivel de agua de 0.504m a la izquierda de la presa y 0.003m a la derecha. Todos los contornos son paredes sólidas excepto el lado de la derecha (Fig. 1) por donde el flujo sale libremente. El coeficiente de Manning es n=0.01.
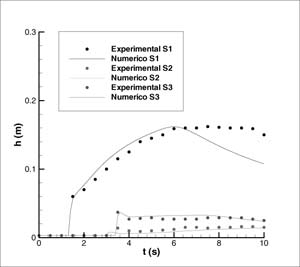
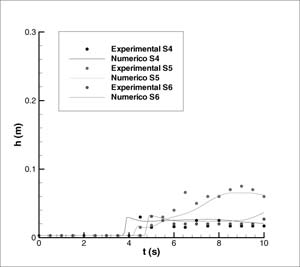
FIGURA
2. Medidas experimentales y resultados numéricos obtenidos con el
esquema upwind en la evolución temporal de la onda producida por una
rotura de presa en un canal que desemboca en una llanura de inundación
En la Fig. 2 se presenta la comparación de las medidas experimentales con los resultados numéricos. Se presenta la evolución temporal durante 10s de la altura de agua en diferentes puntos sonda donde se han tomado medidas experimentales. El primer punto S1 se encuentra situado aguas abajo de la presa. Los puntos S2, S3, S4, S5 y S6 se encuentran en la llanura de inundación como se indica en la Fig. 2. En la Fig. 3 se representan las líneas de nivel, vectores de velocidad y superficie libre respectivamente en los instantes de tiempo T=5 y 10s.
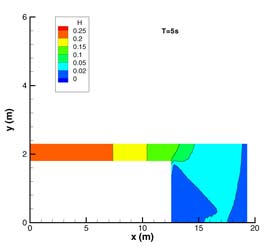
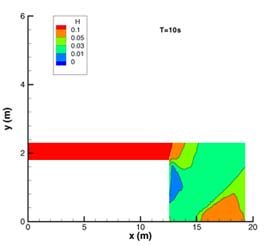
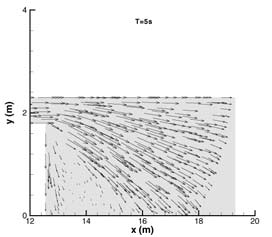
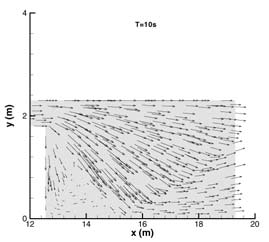
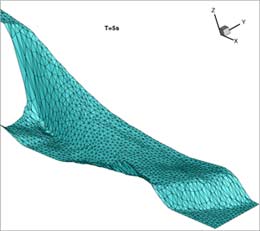
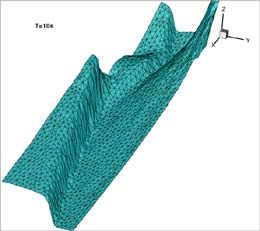
FIGURA
3. Líneas de nivel, vectores de velocidad y superficie librepara
los tiempos T= 5 y 10 s de la onda producida por una rotura de presa en un canal
que desemboca en una llanura de inundación
El modelo físico reducido en el que se basa este caso test fue construido para reproducir una longitud de 5km del valle del río Toce que se encuentra situado en la parte norte de los Alpes italianos. Este modelo ha sido construido por el laboratorio de Investigación Hidráulica de ENEL en Milán (Italia). Debido a la morfología de las secciones transversales del contorno y las pendientes, el flujo aguas arriba en la entrada y aguas abajo en la salida del valle se encuentra en condiciones críticas y, por lo tanto, las condiciones fuera de este tramo de valle no se consideran. La escala del modelo es de 1:100 y la superficie total que ocupa el modelo físico es 55 x 13m. Cuenta con un circuito cerrado de agua con depósitos de entrada y salida y una bomba que, como máximo, puede suministrar al valle un caudal de 500l/s. Las alturas de agua se han medido con transductores de presión y con sondas de nivel.
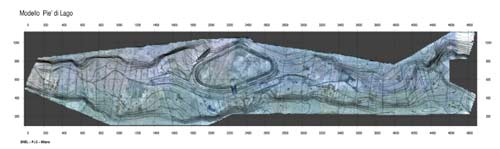
FIGURA 4. Vistaaérea del modelo físico del río Toce


FIGURA 5. Vista general del modelo físico del río Toce
 FIGURA
6. Entrada de agua en el modelo físico del río Toce
FIGURA
6. Entrada de agua en el modelo físico del río Toce
Aumentando la altura de agua de un tanque situado en la primera sección transversal del modelo, se simula experimentalmente una avenida causada por una rotura de presa. El tanque, que se alimenta con una bomba, no se construyó a escala y por tanto no intenta simular el depósito del embalse real. Este hecho, junto a la forma particular en que los datos del hidrograma fueron proporcionados, producen algunas dificultades a la hora de reproducir experimentalmente el flujo de entrada. También influirán en los resultados la no simulación de estructuras presentes en el modelo físico (edificios y dos puentes) que agravan las diferencias entre las medidas y los resultados numéricos.
Las condiciones iniciales son de entrada de flujo por la primera sección con valores proporcionados por un hidrograma y un limnigrama y de lecho seco en todo el valle y también dentro del depósito adyacente (Fig. 7). La avenida se simula numéricamente imponiendo las condiciones de entrada de flujo en la primera sección transversal del valle por medio de un hidrograma. La salida de flujo se considera libre, es decir condiciones supercríticas. El coeficiente de Manning sugerido es 0.0162.

FIGURA
7. Detalle del depósito adyacente en el modelo físico del
río Toce
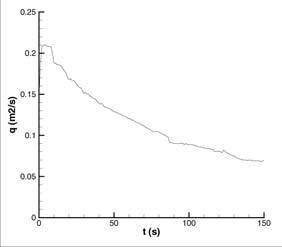
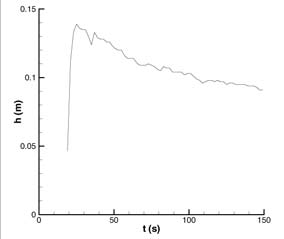
FIGURA
8. Hidrograma (izquierda) y limnigrama (derecha) de entrada en el modelo
físico del río Toce que simula la avenida
En la Fig. 8 se muestra el hidrograma y el limnigrama de entrada en la sección primera del modelo físico que simula una avenida y, a continuación, veremos cómo evoluciona esta onda a lo largo del modelo físico del río.
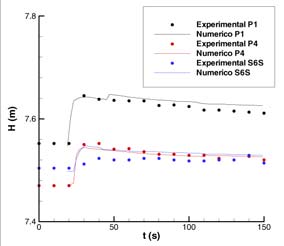
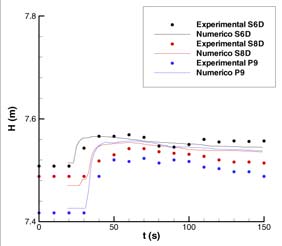
FIGURA
9. Comparación de las medidas experimentales con los resultados numéricos
de la evolución temporal del hidrograma de avenida en algunos puntos
de sonda
En la Fig. 9, se comparan las medidas experimentales con los resultados numéricos obtenidos en la evolución temporal de la onda de inundación en los puntos sonda. La variable representada es H la cota de la superficie libre porque es la variable de la que se disponen medidas.
El tiempo de llegada de la onda se predice correctamente como se observa en la comparación con las medidas experimentales. En cuanto a la altura de agua en los puntos de medida los resultados numéricos se ajustan de forma correcta a la curva experimental. Las posibles diferencias creemos que son debidas a la existencia de un puente que no ha sido simulado en el modelo numérico y que se considerará en un trabajo posterior.
La inundación en el valle se produce al aumentar la altura de agua que proporciona la bomba en el tanque y propagarse ésta sobre el fondo del valle. A continuación, en la Fig. 10, se muestran dos instantáneas de la situación de la avenida en los tiempos T=40s y T=70s donde se han representado líneas de iso-calado y superficie libre. Se ha controlado la pérdida de masa de agua como medida de control del error numérico que se estaba cometiendo y el máximo ha sido de un 2%.
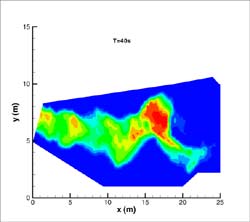
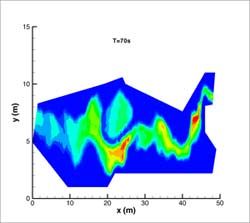
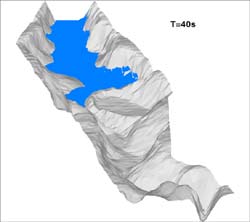
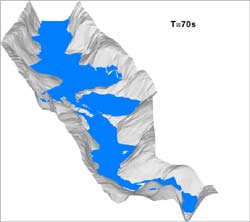
FIGURA
10. Líneas de iso-calado y superficie libre en T= 40 s y T= 70 s
en el modelo físico del río Toce tras una avenida
Se ha mostrado el funcionamiento de una técnica de simulación de flujos de tipo aguas poco profundas en dos ejemplos de régimen transitorio. Está basada en esquemas descentrados sobre volúmenes finitos no estructurados.
El modelo de simulación numérica que se presenta en este trabajo se ajusta adecuadamente a los ejemplos de validación de códigos de este tipo propuestos por un foro internacional interesado en la simulación numérica de ondas bruscas generadas por roturas de presa. Se describe satisfactoriamente el avance de los frentes de onda principales a pesar de que los flujos rápidos violan localmente las hipótesis del modelo matemático empleado. El segundo caso presentado representa una simulación ambiciosa por la irregularidad de la topografía y permite concluir que el modelo propuesto en este trabajo es apto para estudios de este tipo.
Se trata de un modelo universitario propio en desarrollo que, en la actualidad, no se encuentra adaptado a una explotación comercial, pero que puede competir con otros productos similares de software extranjero aliviando la actual dependencia que hay en España de tales códigos. La inclusión de estructuras como puentes, vertederos y otros elementos internos, así como la optimización de la velocidad de cálculo son los objetivos a cubrir en un futuro inmediato.
[1] A. Betamio de Almeida y A. Bento Franco. Modeling of dam break flows. Computational modeling of free surface and pressurized flows. NATO ASI Series, Ed. M.H. Chaudhry y L.W. Mays, 1993.
[2] P. Brufau y P. García Navarro.Two-dimensional dam break flow simulation. Int. J. Num. Meth. Fluids, 33:35-57, 2000.
[3] V. Casulli. Semi-implicit finite difference methods for the two dimensional shallow water equations. J. Comp. Phys., 86:56-74, 1990.
[4] J.A. Cunge, F.M. Holly y A. Verwey. Practical aspects of computational river hyraulics. Pitman Pub. Inc., 1989.
[5] T. Estrela y L. Quintas. El modelo de flujo bidimensional GISPLANA. CEDEX Ingeniería Civil, 104:13-21, 1996.
[6] R. García y R.A. Kahawita. Numerical solution of the St. Venant equations with the MacCormack finite difference scheme. Int. J. Num. Meth. Fluids, 6:259-274, 1986.
[7] P. Glaister. Approximate Riemann solution of the two-dimensional shallow water equations. J. Eng. Math., 24(1):45-53, 1990.
[8] N. Katopodes y T. Strelkoff. Computing two dimensional dam break flood waves. ASCE J. Hyd. Eng., 104:1269-1288, 1978.
[9] N. Katopodes. Two dimensional surges and shocks in open channels. ASCE J. Hyd. Eng., 110:794-812, 1984.
[10] M. Louaked y L. Hanich. TVD scheme for the shallow water equations. J. Hyd. Res., 36:363-378, 1998.
[11] P. Molinaro. Dam break analysis: a state of the art. Comp. Water Res., 1991.
[12] P.L. Roe. Discrete models for the numerical analysis of time-dependent multidimensional gas dynamics. J. Comp. Phys., 63:458-476, 1986.
[13] P.L. Roe. A basis for upwind differencing of the two-dimensional unsteady Euler equations. Num. Meth. Fluid Dyn., 2:55-80, 1986.
[14] M.E. Vázquez Cendón. Estudio de esquemas descentrados para su aplicación a las leyes de conservación hiperbólicas con términos fuente. Tesis Doctoral, Univ. de Santiago de Compostela, 1994.
| SUMARIO | |